VSports app下载 - Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The . gov means it’s official. Federal government websites often end in . gov or . mil VSports app下载. Before sharing sensitive information, make sure you’re on a federal government site. .

Https

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely. V体育官网.

. 2015 Jun 11;10(6):e0128565.
doi: 10.1371/journal.pone.0128565. eCollection 2015.

Emergent Self-Organized Criticality in Gene Expression Dynamics: Temporal Development of Global Phase Transition Revealed in a Cancer Cell Line

Masa Tsuchiya  1 , Alessandro Giuliani  2 , Midori Hashimoto  3 , Jekaterina Erenpreisa  4 , Kenichi Yoshikawa  5
Affiliations

Emergent Self-Organized Criticality in Gene Expression Dynamics: Temporal Development of Global Phase Transition Revealed in a Cancer Cell Line

Masa Tsuchiya et al. PLoS One. .

Abstract

Background: The underlying mechanism of dynamic control of the genome-wide expression is a fundamental issue in bioscience. We addressed it in terms of phase transition by a systemic approach based on both density analysis and characteristics of temporal fluctuation for the time-course mRNA expression in differentiating MCF-7 breast cancer cells. VSports手机版.

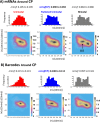
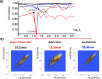
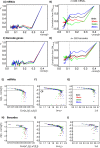
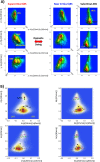
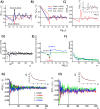
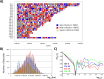
Methodology: In a recent work, we suggested criticality as an essential aspect of dynamic control of genome-wide gene expression. Criticality was evident by a unimodal-bimodal transition through flattened unimodal expression profile. The flatness on the transition suggests the existence of a critical transition at which up- and down-regulated expression is balanced. Mean field (averaging) behavior of mRNAs based on the temporal expression changes reveals a sandpile type of transition in the flattened profile V体育安卓版. Furthermore, around the transition, a self-similar unimodal-bimodal transition of the whole expression occurs in the density profile of an ensemble of mRNA expression. These singular and scaling behaviors identify the transition as the expression phase transition driven by self-organized criticality (SOC). .

Principal findings: Emergent properties of SOC through a mean field approach are revealed: i) SOC, as a form of genomic phase transition, consolidates distinct critical states of expression, ii) Coupling of coherent stochastic oscillations between critical states on different time-scales gives rise to SOC, and iii) Specific gene clusters (barcode genes) ranging in size from kbp to Mbp reveal similar SOC to genome-wide mRNA expression and ON-OFF synchronization to critical states. This suggests that the cooperative gene regulation of topological genome sub-units is mediated by the coherent phase transitions of megadomain-scaled conformations between compact and swollen chromatin states V体育ios版. .

Conclusion and significance: In summary, our study provides not only a systemic method to demonstrate SOC in whole-genome expression, but also introduces novel, physically grounded concepts for a breakthrough in the study of biological regulation. VSports最新版本.

PubMed Disclaimer

Conflict of interest statement (V体育ios版)

Competing Interests: The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Criticality mirrored by the unimodal-bimodal transition through the flattened unimodality.
Criticality of the whole expression at 10–15 min of MCF-7 cell stimulated by HRG exhibits three distinct response domains going from higher to lower nrmsf (left to right in the figure): (left) dynamic domain (nrmsf> 0.16; unimodal profile: N = 3269 mRNAs), (middle) transit domain (0.08 <nrmsf< 0.16 flattened unimodal profile: N = 9707 mRNAs), (right) static domain (nrmsf < 0.21; bimodal profile: N = 9059 mRNAs). First row shows the corresponding putative energy profiles (x-axis: states; y-axis: energy, here specified in abstract terms referring to a physical system undergoing a transition) from a single-well to double-well profiles through flattened single-well profile (blue: 10 min; 15 min: red). These energy profiles should correspond to free energy in terms of the symmetry argument of Landau. Second row shows frequency distributions of mRNA expression from unimodal to bimodal distribution through a flattened unimodal distribution (b: Sarle's bimodality coefficient; x: natural log of expression, ln(ε(t)) and y: natural log of frequency; blue polygonal line: 10 min; red histogram: 15 min); Third row reports the density profile in the regulatory space (x: natural log of expression, ln(ε(10min)) at 10 min vs. y: log of the change in expression at 10–15 min, ln(ε(15min)/ε(10min))) showing clear unimodal to bimodal transition (color bars: probability density). Match of peaks of the histograms and density profiles confirms the statistical reliability of the unimodal-bimodal transition of frequency distribution. The temporal invariant flatness of energy profile suggests the existence of the critical point (CP) (ln(ε(CP)), black solid circle), which is the point where up- and down-regulation balance, i.e., the point where the change in expression between different time points is around zero.
Fig 2
Fig 2. Mean field behavior of the whole mRNA expression and sandplie type singular behaviors.
Dynamic emergent averaging behavior (DEAB) of the expression (mean field behavior) reveals a unimodal to bimodal transition through a flattened unimodality: A) Scattered single mRNA expression (orange dot) overlays with DEAB of the expression (black solid dot) for the HRG response of MCF-7 cells at 15 min on a space spanned by ln(ε(15min)) and ln(1-nrmsf) with the region of nrmsf for three critical states. DEAB of the expression presents ensemble of points, {<nrmsf>, ln<ε(15min)>} (group size: n = 440 mRNAs). B) The difference of points between neighboring group sizes: D(n;n-1) = {(x n−x n-1) + (y n−y n-1)} converges to zero for three points (1: red, 2: blue, 3: purple) on DEAB (n> 50), which depicts the law of large numbers in statistics in that average value converges into a certain value as the ensemble size, n is increased. The x-axis represents group size, n and the y-axis represents D(n;n-1). An initial element of a group (n = 1) builds from its highest nrmsf. C) Frequency (histogram with bin = 0.1) distribution of three group points (1, 2, 3) on DEAB reveals a unimodal (1: b = 0.43) to bimodal (3: b = 0.70 >5/9) transition through a flattened unimodality (2: b = 0.49), where b is Sarle's bimodality coefficient for a finite sample when b> 5/9 may indicate a bimodal or multimodal distribution. The result shows that a transition point exists at a flattened profile. Sandpile type singular behaviors are revealed from grouping by expression change: D) The grouping of mRNA expression (different mean-field from one based on nrmsf) at t = t j according to the degree of expression change at t j+1 –t j (j = 10, 15, 20, 30 min) reveals a sharp transition similar to the sandpile model—top row for mRNAs (group size: n = 440), and middle row for barcode genes (n = 182; refer to Fig 8) overlaying with single expression distribution (orange: mRNA; red: barcode). On the contrary, randomized barcode genes (n = 78; random barcode II; see the main text) show no evidence of transition (bottom row; green: single barcode) in the expression vs. expression change plane. Left panels: 10 min vs. 10–15 min; Middle panels: 15 min. vs. 15–20 min.; Right panels: 20 min. vs. 20–30 min, <> represents simple arithmetic mean over an ensemble or a group.
Fig 3
Fig 3. Self-similar power law behavior around CP of mRNA expression and barcode genes.
Panel A): First row- frequency distribution (bin size = 0.1) of mRNAs (n = 440 mRNAs) at 10 min shows a unimodal to bimodal change around critical point (0.090 <nrmsf< 0.092). The x-axis represents the natural log of mRNA expression, ln(ε(10min)) for a specific range of nrmsf: unimodal (left panel: 0.105 <nrmsf< 0.109), flattened unimodal (middle panel: 0.090 <nrmsf< 0.092), and bimodal (right panel: 0.084 <nrmsf< 0.086). The y-axis represents frequency of expression. Second row- the corresponding probability density profile in the regulatory space—expression vs. expression change in log scale with probability density (color bars) confirms the unimodal to bimodal transition through flattened unimodality, where a black arrow points to the bifurcation of low-expression state (LES). Panel B): First row—the frequency distribution of barcode genes (n = 182 barcodes) shows a unimodal to bimodal change around a critical point (0.108 <nrmsf< 0.112) for unimodal (left), flattened (middle) and bimodal (right) distributions. Second row—this is confirmed by probability density profile in the regulatory space. Both mRNAs and barcode genes on chromosomes reveal the existence of self-similar power law (scaling) behavior around CP analogous to that of the whole mRNA expression (see Fig 1), which is an essential characteristic of SOC.
Fig 4
Fig 4. The early stage of a singular response.
Panel A) shows the Pearson correlation (dashed line: P(t 0;t j)) between the t 0 expression profile and the expression profiles at increasing time. Solid line reports the correlation between neighboring temporal expression profiles (P(t j;t j+1)) relative to different characteristic domains (x: common logarithm of minutes; y: correlation value). Correlation dynamics reveal a sharp cleft at 15–30 min in the dynamic domain (super-critical: red) with less and slight effects on the transition (near-critical: blue) and static (sub-critical: black) domains, respectively. Panel B) shows that the singular response is due to the bifurcation of a coherent expression state (CES indicated by a black arrow, equivalent to HES2 in Fig 6A: right panel) at 15–20 min and its annihilation at 20–30 min (left: 10 min vs. 15 min; middle; 15 vs. 20 min; right; 20 min vs. 30 min in expression). This is related to the fast /short-span mode in SOC (see the main text).
Fig 5
Fig 5. Emergent avalanche like distribution on between-profiles correlation analysis of expression groups.
Whole mRNA expression (unit: mRNA) and barcode genes (unit: barcode gene; refer to the main text) are sorted and grouped (group size: 440 mRNAs; 182 barcodes) according to the degree of nrmsf. In A-D, the y-axis shows the degree of correlation of fluctuations from the initial point and the x-axis shows <nrmsf>: ensemble average of nrmsf. Correlations (0 min: black; 10 min: red; 15 min: green; 20 min: blue) were computed according to different scaling options (see the main text): A) Correlation scaled from the center of mass of the group (CMgroup) (Pearson correlation: r). Correlations fluctuate around zero, indicating that expression is stochastic in nature. B) Correlation from the center of mass of the whole expression (CMwhole). A focal point (FP) is present, where the correlations converge at around the middle of the groups, and at this point their trends invert and start to diverge. This inversion reveals clear coupling with opposite coherent stochastic oscillations of the ensemble of expressions above and below the focal point (see the main text). Similar behavior is evident for barcode genes in C), in which correlations are scaled from CMgroup, and D) which in turn is scaled from CMwhole. Dashed vertical lines in C) and D) show average nrmsf of CP (<nrmsf>CP) of mRNA and barcode genes over 10, 15 and 20 min, respectively are almost matched to nrmsf of FP, where average <nrmsf>CP is 0.09 and 0.11 for mRNA and barcode gene, respectively. In E-G (first row: N = 22035 mRNAs), and H-J (second row: N = 7286 barcodes), the y-axis represents natural log of 1- <nrmsf>, ln(1- <nrmsf>). The x-axis represents left (E and H): the correlation with no scaling between groups at t = t j between the highest nrmsf group (expression vectors: x 1 (t j), x B 1(t j) for mRNA and barcode gene, respectively) and the i th group (x i(t j) and x B i(t j)); center (F and I): natural log of the average expression of a group (ln(<ε>) for mRNA and ln<ε B> for barcode gene, which show DEAB of the expression; right (G and J): the bimodality coefficient (1-b, and b: Sarle's bimodality coefficient) for mRNA expression and barcode genes, respectively. All figures for mRNA and barcodes show scaling-divergent behaviors, where CP shown by dashed horizontal lines (1- <nrmsf>CP) is at onset of the divergent point. This exactly reveals the characteristics of avalanche like distribution in the sandpile model of SOC. The power law scaling behaviors (F and I) on DEAB of the expression for mRNAs and barcode genes are revealed in the form of 1- <nrmsf> = < ε >-β: α = 1.27 & β = 0.16 (p< 10−14) and α = 1.37 & β = 0.21 (p< 10−6), respectively, which indicates similar SOCs of the mRNA (each gene contributes to the model) and barcode (the barcodes as single units) representations.
Fig 6
Fig 6. Anti-phase behavior of autonomous bistable switches (ABSs) between super- and sub-critical states.
A) Pseudo-3-D probability density profiles on the regulatory space show the opposite ON-OFF oscillation of coherent expression states (low- and high-expression states (LES and HES) with x = 0 (marked by a vertical dashed line) in ABS between super- and sub-critical & near- critical states (left column: ABS of super-critical; center: near-critical: right: sub-critical). The x-axis shows the (natural log) expression change at 10–15 min (first row), 15–20 min (second), and 20–30 min (third); the y-axis shows the (natural log) expression for 10 min (first row), 15 min (second), and 20 min (third). In the super-critical ABS, LES2 is bifurcated at 15 min, becomes HES2 at 20 min, and annihilated at 30 min (refer to Fig 4B). B) Sensitivity to the initial conditions of the temporal dynamics of groups of mRNAs at different expression initially localized around x = 0 (indicated by purple, green, blue and red squares; left top) in a sub-critical ABS represented as a 2-D density profile (N = 9059 mRNAs). The groups refer to two coherent expression states–two groups are in a high-expression state (HES1), the other two in a low-expression state (LES1)—of the sub-critical ABS on the regulatory space (left top: 0–10 min vs. 10 min; right top: 10–15 min vs. 15 min; left bottom: 15–20 min vs. 20 min; right bottom: 20–30 min vs. 30 min). The figure reveals amplification in the expression change (x-axis) but not in expression (y-axis). This behavior indicates a highly correlative behavior for expression and stochastic resonance effect for the expression change. The black solid dot indicates the center of mass of sub-critical ABS(CMsub).
Fig 7
Fig 7. Coupling between fast and slow modes of coherent stochastic oscillation (CSO).
CSO is appreciated in terms of Pearson correlations (x: common logarithm of minutes): A) between expression (at t = t j) and the expression change (change in expression from t j to t j+1; j = 1,..,17), P(t j;t j+1−t j)) and B) in the difference in expression between 0–10 min and t j+1−t j, P(t 1 −t 0;t j+1−t j). In A), an opposite response is seen between the super-critical state (red line) and sub-critical (black) & near-critical (blue) states, which shows that the opposite coherent oscillatory dynamics of ABS continue, whereas B) shows the loss of the initial memory of the expression change (0–10 min), which confirms that the change in expression is stochastic. The x-axis represents log10(t j[min]). C): Temporal change in expression of the center of mass of ABSsub (x(CMsub)) shows, albeit with slight oscillation around zero, a good correlation with the Pearson correlation, P(t j;t j+1 - t j) of ABSsub (upper right; x(CMsub) by red dot), which reveals an algebraic correlation to the dynamics of CMsub as a feature of SOC (see the main text for details), where the scaled motion of CMsub (upper right) is multiplied by αN(tj)N(tj+1−tj), where α = 1.45 and N(t j) and N(t j+1 − t j) are normal to the expression vector at t = t j and the vector of the expression change: t j+1 −t j. D): The long-span opposite dynamics shown in A) appear as an opposite sign of the Pearson correlation of CM between super- and sub-critical states. The average Pearson correlation (over 200 repeats; black dot) of the CM of a randomly selected temporal change in expression (t j+1−t j) from each critical state converges to r = -0.927 (x: m randomly selected mRNAs vs. y: Pearson correlation coefficient). E) Average Pearson correlation of expression (blue) and the change in expression (green) for random sampling (m = 100 with 200 repeats) between two critical states exhibits a similar singular fast/ short span correlation to the super-critical state at 15–30 min with no apparent subsequent response, which is confirmed by F): The figure reports converging Euclidean distance of two correlation points (x: time; y: correlation) between m and m+1 random samplings to zero as m is increased. This suggests the existence of coupling between a fast short span mode in the super-critical state and a long span coherent oscillation in the sub-critical state. G) and H): The emergence of coherent oscillation and stochasticity is examined in terms of G): the difference (Δ) of Pearson correlation, P(t j;t j+1−t j) between ABSsub(t j ; t j+1−t j) and m randomly selected mRNAs and H): the difference in P(t 1 −t 0;t j+1−t j) of m randomly selected mRNAs with 400 repeats for each choice, respectively (t 0 = 0 min: black, t 1 = 10 min: red, t 2 = 15 min: green, t 3 = 20 min: blue), where the standard deviation (SD) for time points (j = 1,2,3) follows α/m scaling: α is 0.77 and 1.0 for coherence and stochasticity (in the inset figure in the upper-right corners; red: scaling; black: SD of j = 1), respectively. The results indicate the emergence of CSO after around m = 50, which is also supported by the random sampling results given in D) and F) (marked by black vertical dashed lines).
Fig 8
Fig 8. Barcode genes and temporal response of super-critical genes on chromosomes.
A) Genes of critical phases are mapped into a human chromosome (UCSC hg19), corrected for the multiplicity of probes (mRNA expression) such as multiple probes of a gene due to an mRNA variant; the x- and y-axes show the chromosome position and chromosome number including X and Y chromosomes, respectively. Based on the distinct physical properties of the critical states, genes on a chromosome are clustered to form barcode genes (yellow: super-critical (N = 1262); red: near-critical (N = 3072); blue: sub-critical (N = 2952); gray: the unknown chromosome region), where the boundary of a barcode is defined as when two neighboring genes belong to different critical states; for instance, a sequence of.. S-S-S-T-T-S.. has two barcode genes, S-S-S and T-T; D: dynamic domain: super-critical; T: transit domain: near-critical; S: static domain: sub-critical (the plot was provided by I. E. Motoike). B) Frequency distribution of the correlation length of barcode genes for critical phases (the colors are the same as those in the barcode) shows the size of barcode genes within the range from kbp to Mbp for all states. The correlation length is estimated as the base length from the start codon of the initial gene to the end codon of the last gene within a barcode; the x- and y-axes show the common logarithm of a base pair and the number of barcodes (bin size: one-tenth of a unit length). C) Pearson correlation, P(t 0;t j) of super-critical genes on chromosomes, which shows temporally four most responsive chromosomes (chromosome 2: black, 14: blue, 16: red, 19: green) with the singular like responses at 15–30 min (see also Fig 4A). The x-axis represents log10(t j[min]).
Fig 9
Fig 9. Synchronization of barcode genes on chromosomes with mRNA coherent expression dynamics.
Panel A): super-critical state, Panel B): sub-critical state for barcode genes. The panels present the probability density functions of barcode genes on the regulatory space (first row: x: change in the natural logarithm of expression at 10–15 min; y: natural logarithm of expression at 10 min); second row: x: change at 15–20 min; y: at 15 min; third row: x: change at 15–20 min; y: at 20 min), showing a similar opposite oscillation between sub-critical and super-critical states in mRNA expression dynamics (Fig 6A). Panels C-E): mRNAs versus barcode genes. Panels F-H): a variety of barcode genes. Temporal Pearson correlations for sub-critical as well as near-critical barcode genes confirm the ON-OFF synchronization with mRNA expression dynamics, the same in terms of stochasticity and coherent oscillation (coherent stochastic oscillation: CSO; D: stochasticity; E: coherent oscillation), whereas super-critical barcodes reveal the opposite phase of CSO, showing similar temporal trend to critical states of mRNA (mRNAs (dark colors): subcritical: black; near-critical: blue; super-critical: red; barcodes: the corresponding lighter colors). Panels C & F: Pearson correlation, P(t 0;t j); Panels D & G: P(t 1-t 0;t j+1 -t j), and Panels E & H: P(t j;t j+1−t j). Temporal Pearson correlations (F-H) confirm that barcodes without single gene (multiple genes: dashed lines) clearly follow similar trends of temporal correlations of the whole barcodes of critical states (solid lines), and thus similar correlation response to the mRNA dynamics. Correlation trends of barcodes are shown to be clearly distinct from random-barcodes: one (green dotted line: random-barcode I) for average value of randomly selected barcodes (n = 200) out of the whole barcodes combining critical states with 100 repeats–forming Gaussian distribution, and another (brown dotted line: random-barcode II) for barcode genes (N = 3130) of randomly mixed critical states, where genes on chromosome are randomly selected, and for each selected barcode, the number of elements is assigned randomly from 1 to 4 neighboring genes.
Fig 10
Fig 10. Genome-wide attractor on mRNA expression vector field.
First row: profile-correlation of the whole expression between different time points (left: 10 min vs. 15 min; right: 15 min vs. 20 min) have a near to unity correlation—Pearson correlation coefficient, r = 0.98 in 10 min vs. 15 min (left), r = 0.94 in 15 min vs. 20 min (right). Each point represents single expression point, (x i(t j) = ln(ε(t j)), y i(t j) = ln(ε(t j+1)) (i = 1,..N = 22035), where ln(ε(t j)) is natural log of mRNA expression at t = t j (t j = 10 min, 15 min). The near to unity correlations between gene expression profiles coming from the same tissue implies that the global order of expression across different genes is largely invariant and is statistically very reliable. Second row: a stream plot (using Mathematica 10) is generated from vector field values {Δx i(t j), Δy i(t j)} given at specified expression points {x i(t j), y i(t j)}, where Δx i = x i(t j+1)- x i(t j), Δy i = y i(t j+1)- y i(t j). Streamlines of the whole expression vector field (blue lines) are generated and a yellow arrow represents a vector at a specified expression point (plotting every 20th point). The result shows a clear “genome-wide attractor”—an attractor set is represented as a manifold (linear line: y = rx) in the space spanned by the whole mRNA expression of different time points, which suggests temporal invariance of whole-expression profiles acting as genome-wide attractors.
See this image and copyright information in PMC

References

    1. Klevecz RR, Bolen J, Forrest G, Murray DB (2004) A genomewide oscillation in transcription gates DNA replication and cell cycle. Proc Natl Acad Sci USA. 100: 1200–1205. - PMC (VSports) - PubMed
    1. Takahashi K, Yamanaka S (2006) Induction of pluripotent stem cells from mouse embryonic and adult fibroblast cultures by defined factors. Cell 131: 861–872. - PubMed
    1. Young RA (2011) Control of the embryonic stem cell state. Cell 144: 940–945. 10.1016/j.cell.2011.01.032 - DOI (VSports) - PMC - PubMed
    1. Raser JM, O’Shea EK (2005) Noise in gene expression: Origins, consequences, and control. Science 309: 2010–2013. - PMC - PubMed
    1. Yoshikawa K (2002) Field hypothesis on the self-regulation of gene expression. J Biol Phys 28: 701–712. 10.1023/A:1021251125101 - DOI - PMC - PubMed

Publication types (VSports手机版)