CAUSAL GRAPHICAL MODELS IN SYSTEMS GENETICS: A UNIFIED FRAMEWORK FOR JOINT INFERENCE OF CAUSAL NETWORK AND GENETIC ARCHITECTURE FOR CORRELATED PHENOTYPES (V体育安卓版)
- PMID: 21218138
- PMCID: VSports最新版本 - PMC3017382
- DOI: 10.1214/09-aoas288
CAUSAL GRAPHICAL MODELS IN SYSTEMS GENETICS: A UNIFIED FRAMEWORK FOR JOINT INFERENCE OF CAUSAL NETWORK AND GENETIC ARCHITECTURE FOR CORRELATED PHENOTYPES
Abstract
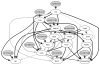
Causal inference approaches in systems genetics exploit quantitative trait loci (QTL) genotypes to infer causal relationships among phenotypes. The genetic architecture of each phenotype may be complex, and poorly estimated genetic architectures may compromise the inference of causal relationships among phenotypes. Existing methods assume QTLs are known or inferred without regard to the phenotype network structure. In this paper we develop a QTL-driven phenotype network method (QTLnet) to jointly infer a causal phenotype network and associated genetic architecture for sets of correlated phenotypes VSports手机版. Randomization of alleles during meiosis and the unidirectional influence of genotype on phenotype allow the inference of QTLs causal to phenotypes. Causal relationships among phenotypes can be inferred using these QTL nodes, enabling us to distinguish among phenotype networks that would otherwise be distribution equivalent. We jointly model phenotypes and QTLs using homogeneous conditional Gaussian regression models, and we derive a graphical criterion for distribution equivalence. We validate the QTLnet approach in a simulation study. Finally, we illustrate with simulated data and a real example how QTLnet can be used to infer both direct and indirect effects of QTLs and phenotypes that co-map to a genomic region. .
VSports手机版 - Figures
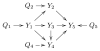
"VSports手机版" References
-
- Banerjee S, Yandell BS, Yi N. Bayesian QTL mapping for multiple traits. Genetics. 2008;179:2275–2289. - V体育ios版 - PMC - PubMed
-
- Broman K, Wu H, Sen S, Churchill GA. R/qtl: QTL mapping in experimental crosses. Bioinformatics. 2003;19:889–890. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources (VSports app下载)
Other Literature Sources
